Das Yin und Yang medizinisch-diagnostischer Tests
Ob Gendiagnostik, Brustkrebs oder HIV: Kommt ein neuer diagnostischer Test auf den Markt, berichten Medien gerne über die neuen Chancen, eine Krankheit frühzeitig zu erkennen und zu behandeln. Im Versuch, einen solchen Test einzuordnen, berichten Journalisten gerne von „zuverlässigen Testergebnissen“ oder „hoher Aussagekraft“ ohne dies durch konkrete Werte zu illustrieren. Damit lassen sie Rezipienten im Unklaren, und machen sich zum verlängerten Arm der Marketingabteilung. Wir erklären in diesem Text, welche Werte wichtig sind, welche von Experten abgefragt werden müssen und wie Journalisten diese den Rezipienten erklären können.
Wie gut ein diagnostischer Test ist, ist eine der ersten Fragen, die aufkommen, wenn ein (neues) Verfahren Schlagzeilen macht. Dabei interessiert in erster Linie, wie genau der Test Betroffene von Gesunden unterscheiden kann. Wie viele HIV-Infizierte bleiben unentdeckt, obwohl sie den Test machen? Und wie oft wird fälschlicherweise Alarm geschlagen? An der Stelle genügt es nicht, von zuverlässigen Ergebnissen oder einem neuen Durchbruch zu reden; auch ein einzelner Wert zur Testgenauigkeit reicht nicht aus, um die diagnostische Testgüte ausreichend zu beschreiben. Vom Journalisten wird erwartet, dass er bestimmte Parameter nennt – und diese in nachvollziehbaren Zahlen und Begriffen darstellt.
Sensitivität und Spezifität…
HIV ist ein gutes Beispiel für eine Erkrankung, die möglichst früh angemessen behandelt werden sollte. Deshalb interessiert die Medizin, wie viele der Infizierten durch einen HIV-Test erkannt werden können. Informationen dazu liefert die Sensitivität eines diagnostischen Testes. Sie gibt den Anteil der richtig Positiven an allen Erkrankten an, also die Wahrscheinlichkeit, mit welcher ein diagnostischer Test Kranke bzw. Betroffene auch als krank/betroffen identifiziert. Soll ein neuer Test eingeführt werden, wird er deshalb zunächst an nachweislich Erkrankten geprüft. Erkennt er beispielsweise 98 von 100 Betroffenen als krank, liegt eine Sensitivität von 98 Prozent vor.
Liefert ein Test ein negatives Ergebnis, möchte der Patient in der Regel auch wissen, wie sicher er sein kann, dass er nicht krank ist. Hier ist die Spezifität die relevante Kenngröße. Sie gibt den Anteil der richtig Negativen an allen Gesunden an, also die Wahrscheinlichkeit, mit der ein diagnostischer Test Gesunde als gesund einstuft. Um diesen Wert zu bestimmen, führen Mediziner den Test in der Evaluierungsphase an einer Gruppe von nachweislich Gesunden durch und bestimmen im Anschluss die Negativrate.
Die Ergebnisse eines Diagnosetestes lassen sich anschaulich anhand einer Vierfeldertafel darstellen:
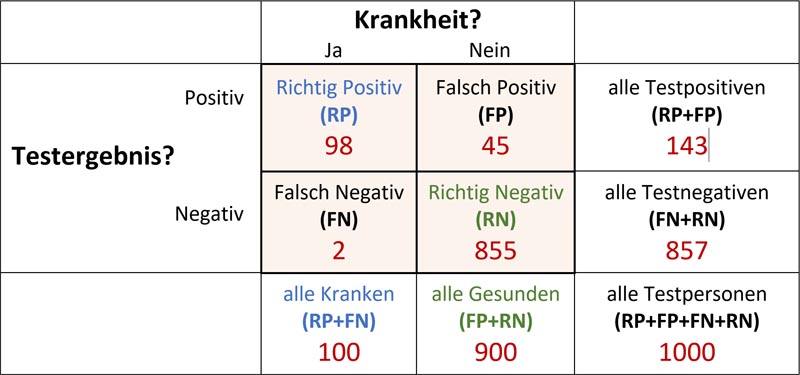
Fallzahlen eines beispielhaften Diagnosetests in natürlichen Häufigkeiten
In unserem Beispiel wurden 1000 Personen getestet, 100 davon haben die Krankheit tatsächlich, 900 haben sie nicht. Von den 100 Betroffenen erkennt der Test 98 und 2 nicht (Spalte 1), von den 900 Gesunden identifiziert 45 fälschlicherweise als krank und 855 als korrekterweise gesund (Spalte 2). Der Test besitzt also eine Sensitivität von RP/(RP+FN) = 98% und eine Spezifität von RN/(RN+FP) = 95%.
Sensitivität und Spezifität beziehen sich auf zwei verschiedene Bezugsgruppen (Kranke und Gesunde) und können deshalb nicht zu einem Wert zusammengefasst werden. Es genügt auch nicht, nur einen der beiden Werte zu nennen. Grundsätzlich gilt: Je höher die Sensitivität eines Verfahrens ist, desto geringer ist die Spezifität und umgekehrt. Diese enge Beziehung der beiden Werte wurde beim amerikanischen HealthNewsReview auch als das „Yin und Yang medizinisch-diagnostischer Testverfahren“ beschrieben.
Das Ziel eines diagnostischen Tests entscheidet letztendlich darüber, wie er aufgebaut wird und ob eher eine hohe Sensitivität oder eine hohe Spezifität gewählt wird. Eine hohe Sensitivität ist vor allem bei Screenings erwünscht, bei denen möglichst alle Betroffenen erkannt werden sollen. Eine hohe Spezifität ist hingegen bei Bestätigungstests erforderlich, die eine Krankheit sicher ausschließen sollen. Häufig werden diese Verfahren kombiniert angewandt, beispielsweise beim HIV-Test, bei dem zunächst eine Untersuchung mit hoher Sensitivität und anschließend eine mit hoher Spezifität durchgeführt wird, bevor der Patient das Testergebnis erfährt.
…sagen nicht alles
Das Ergebnis eines diagnostischen Tests entscheidet unter anderem darüber, ob am Patienten eine bestimmte Maßnahme, wie etwa eine medikamentöse Behandlung, vorgenommen wird oder nicht. Im klinischen Alltag reichen deshalb Sensitivität und Spezifität nicht aus, um zu entscheiden, ob die Durchführung eines diagnostischen Tests Sinn macht. Liegt ein bestimmtes Testergebnis vor, interessiert eher, mit welcher Wahrscheinlichkeit dieses auch richtig ist. Schließlich muss der behandelnde Arzt entscheiden, ob und welche weiteren diagnostischen oder therapeutischen Maßnahmen vorgenommen werden. Auch der Patient möchte verlässliche Informationen über seinen Zustand haben. Wie zuverlässig das Ergebnis ist, hängt allerdings nicht nur von der Testgüte selbst ab. Einen entscheidenden Einfluss hat die Prävalenz, also die Häufigkeit, mit der die Krankheit innerhalb einer Bevölkerungsgruppe auftritt und damit die Wahrscheinlichkeit, überhaupt zu erkranken.
Gerade wenn der Test eine positive Diagnose liefert, der Getestete also möglicherweise erkrankt ist, stehen in der Regel Entscheidungen an. Das kann der Beginn einer belastenden Chemotherapie ebenso wie die schwerwiegende Entscheidung über einen Schwangerschaftsabbruch sein. Aber die Testgüte alleine reicht im individuellen Fall noch gar nicht aus, um zu wissen, wie gut der Test eine Erkrankung anzeigt oder nicht. Es kommt nämlich darauf an, zu welcher Gruppe von Menschen eine Person zählt.
Aufschluss darüber, wie sicher die Person in dem Fall wirklich betroffen ist, liefert der positive prädiktive Wert (PPW). Er gibt an, mit welcher Wahrscheinlichkeit die Person, die ein positives Testergebnis hat, auch tatsächlich krank ist. Anders als die Werte von Sensitivität und Spezifität hängt diese Kenngröße von der Prävalenz, also der Häufigkeit einer Erkrankung innerhalb einer Bevölkerungsgruppe ab. Dabei gilt: Je seltener eine Krankheit ist, desto niedriger ist auch der positive prädiktive Wert.
Positives Testergebnis – Grund zur Panik?
Ein gutes Beispiel, das zeigt, wie wichtig dieser Aspekt ist, bietet der Schnelltest auf HIV. Dieser hat eine besonders hohe Sensitivität, um möglichst keine Infizierten zu übersehen. Die Prävalenz für HIV innerhalb Deutschlands liegt bei etwa 0,1 Prozent, das heißt, eine Person von Tausend ist infiziert, 999 (99,9 Prozent) nicht.
Der Test hat (in diesem Beispiel zu Rechenzwecken) eine Sensitivität von 100 Prozent (tatsächlich ist sie niedriger) und eine Spezifität von 99,7 Prozent. Durch die hohe Sensitivität erkennt er den einen Infizierten von eintausend sicher. Anders verhält es sich mit der Spezifität, die ja nicht ganz so gut ausfällt. Von den 999 Nicht-Infizierten werden 0,3 Prozent (100 Prozent minus Spezifität) fälschlicherweise als positiv eingestuft; die Wahrscheinlichkeit, gesund zu sein und trotzdem ein positives Ergebnis zu erhalten liegt damit bei 99,9 Prozent x 0,3 Prozent = 0,2997 Prozent. Von 1000 getesteten Personen werden also etwa 3 Personen fälschlicherweise als Träger des Virus angezeigt.
Die Zusammenhänge lassen sich auch anhand eines Baumdiagramms veranschaulichen.
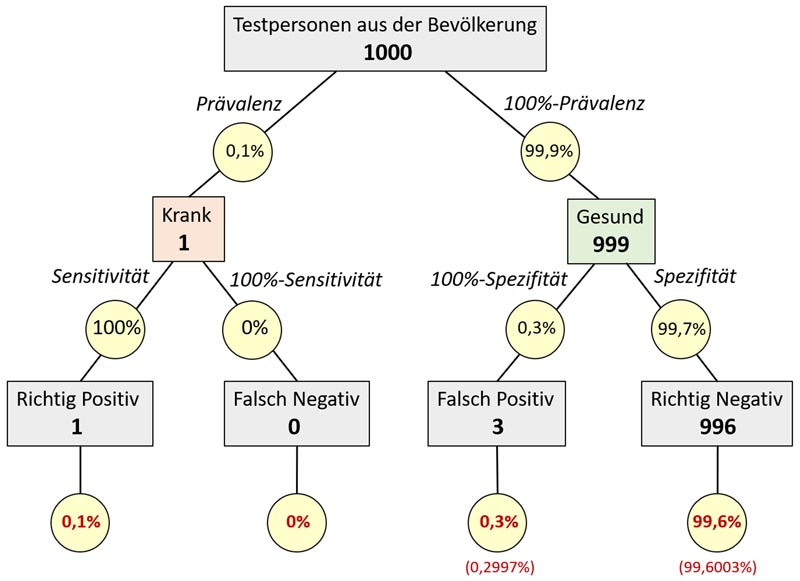
Baumdiagramm zu Testwahrscheinlichkeiten am Beispiel eines HIV-Schnelltests (eigene Abbildung)- „100%-Sensitivität“ und „100%-Spezifität“ sind zu lesen als „100% minus Sensitivität“ und 100% minus Spezifität“.
Der positive prädiktive Wert gibt dann den Anteil von richtig Positiven an allen Testpositiven an. Das wären in dem Fall 0,1%/(0,1% + 0,2997%) ≈ 25%. Oder, grob gesagt, von 4 (1+3) positiv getesteten ist nur einer tatsächlich betroffen.
Jetzt steht in der Packungsbeilage zum HIV-Heimtest aber trotz dieser Zahlen für den Fall einer positiven Anzeige: „Sie sind wahrscheinlich HIV-positiv“. Tatsächlich ist jedoch die Wahrscheinlichkeit, nicht infiziert zu sein, viel höher. In einer Arztpraxis könnte dies nun ein Arzt erklären und einordnen. Bei einem Heimtest fehlt diese Unterstützung indes. Umso wichtiger erscheint es daher, solche Aspekte in der Berichterstattung zu kommunizieren.
Entscheidend ist auch, aus welcher Risikogruppe eine Person stammt, die sich testen lassen möchte. Verschiedene Risikogruppen unterscheiden sich nämlich in der Häufigkeit, in der eine bestimmte Erkrankung innerhalb der Gruppe auftritt. Damit steigt oder fällt die Wahrscheinlichkeit für ein echtes positives Testergebnis.
Die Wahrscheinlichkeiten ändern sich dramatisch, je nachdem zu welcher Risikogruppe eine Person zählt. Innerhalb einer Personengruppe, die ohne nennenswerte HIV-Risikofaktoren, wie etwa homosexuelle Kontakte oder intravenösen Drogenkonsum lebt, herrscht schätzungsweise nur eine Prävalenz von 0,01% – damit ist einer von Zehntausend betroffen. Auf unser obiges Rechenbeispiel angewandt, ist eine Testperson aus dieser Gruppe bei einem positiven Testergebnis sogar nur zu einer Wahrscheinlichkeit von 3,2 Prozent tatsächlich krank. Ganz anders sieht dies beispielsweise bei einer Person mit intravenösem Drogenkonsum aus (geschätzte Prävalenz einer HIV-Erkrankung liegt bei etwa 5 Prozent, d.h. 5 von 100 Drogenabhängigen, die ihre Drogen intravenös nehmen, tragen das Virus im Blut). Wird diese Person positiv getestet, liegt die Wahrscheinlichkeit, tatsächlich mit HIV infiziert zu sein, bereits bei 94,6 Prozent. Von 100 positiv getesteten sind in dieser Risikogruppe also fast 95 Personen tatsächlich infiziert.
Neben dem positiven prädiktiven Wert gibt es auch den negativen prädiktiven Wert. Dieser gibt an, mit welcher Wahrscheinlichkeit eine Krankheit bei negativem Testergebnis ausgeschlossen werden kann. Er berechnet sich aus dem Anteil der richtig Negativen an allen Testnegativen.
Beide Werte lassen sich auch anhand folgender Formeln berechnen (Bayes’sches Theorem), wenn man die Prävalenz sowie die Werte von Sensitivität und Spezifität eines Tests kennt:
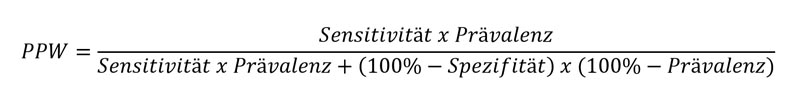
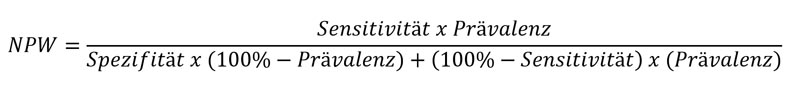
Welche Werte brauche ich jetzt…
Mit Sensitivität, Spezifität und den beiden Vorhersagewerten haben wir vier wichtige Werte in Bezug auf die Aussagekraft von Diagnosetests kennengelernt. Ein entscheidender Schritt fehlt allerdings noch: Diese Werte den Lesern/Zuschauern/Zuhörern auch verständlich zu vermitteln, und zwar so, dass sie Risiken und die Qualität eines Tests richtig einschätzen können.
Dabei gilt: Angaben zu Sensitivität und Spezifität müssen in Artikeln über diagnostische Tests unbedingt vorhanden sein („Yin und Yang“). Finden sich dazu bei der Recherche keine Angaben, etwa weil der Test noch in der Anfangsphase seiner Entwicklung steht, sollte das dem Rezipienten auch offen mitgeteilt werden. Prädiktive Werte können genannt werden – sofern das Sinn ergibt. Dies hängt indes sowohl vom Test als auch der Zielsetzung des Artikels ab. Hat ein Test eine besonders hohe Falschalarmrate (Falschpositivrate), sollte das durch den positiven prädiktiven Wert kommuniziert werden. Das gleiche gilt im Zusammenhang mit Therapien, die bei falsch-positiven Angaben erheblichen gesundheitlichen Schaden anrichten können, wie etwa bei der Behandlung von Krebs. Auch wenn der Artikel die psychische Belastung bei einem unsicheren positiven Testergebnis thematisiert, kann es hilfreich sein, den PPW zu nennen.
…und wie sage ich das dem Leser?
Vermittelt man Werte zu Diagnosetests an Laien, muss deutlich werden, auf welche Personengruppe sich die Angabe bezieht, die man macht. Bezieht sich die Angabe nur auf die Gruppe der Kranken, wie etwa bei der Sensitivität, bezieht sie sich nur auf Personen mit einem positiven Testergebnis? Sind die Wahrscheinlichkeiten verallgemeinerbar oder gelten sie für Risikogruppen? Natürliche Häufigkeiten sind dabei immer anschaulicher als Einzelfallwahrscheinlichkeiten, die von Lesern zum Teil unterschiedlich interpretiert werden. „Der Test erkennt die Krankheit in 9 von 10 Fällen“ ist deshalb besser als „Der Test erkennt die Krankheit zu 90%“. Dabei sollte als Basis stets die gleiche Bezugsgröße gewählt werden, wie etwa 100, 1000 oder 10.000 Personen. Natürliche Häufigkeiten lassen sich auch gut in einem Baumdiagramm darstellen, wie das obige Beispiel zeigt; sie eignen sich außerdem, um die Vorhersagewerte nachvollziehbar zu bestimmen.
Um zu vermeiden, dass der Leser Risiken oder Effekte falsch einschätzt, sollten in der Berichterstattung nach Möglichkeit nur absolute, keine relativen Größen (Gruppenvergleiche) auftauchen – diese führen nämlich schnell dazu, dass Ereignisse überschätzt werden. Natürlich stimmt es rein mathematisch, dass intravenös Drogenkonsumierende ein 500-mal höheres Risiko für HIV haben als Angehörige der Niedrigrisikogruppe – dennoch ist es hier besser, für jede Gruppe getrennte Angaben zu machen oder sogar beide Angabenformate zu verwenden.
Eine gute Möglichkeit, Sachverhalte verständlich darzustellen und damit auch den Text nicht mit Zahlen zu überlasten, bieten Faktenboxen. In einer Studie konnte das Harding-Zentrum für Risikokompetenz belegen, dass sich der Wissenserwerb von Lesern durch Faktenboxen maßgeblich erhöht und Risiken besser eingeschätzt werden. Gerade Häufigkeiten können in diesem Format anschaulich und vergleichend dargestellt werden – begleitet von einem faktenbasierten Erklärtext. Beispiele, wie solche Faktenboxen aussehen können, sind etwa auf der Webseite des Harding-Zentrums zu finden. Hier haben die Ersteller bereits den gesamten Nutzen eines diagnostischen Testes unter Einbeziehung von Therapiedaten dargestellt, die in diesem Artikel noch nicht thematisiert wurden.
Testgüte ist nicht gleich Nutzen
Wichtig ist, im Hinterkopf zu behalten, dass die hier vorgestellten Parameter zunächst nur etwas über die Aussagekraft eines diagnostischen Tests sagen, nichts aber über seinen tatsächlichen medizinischen Nutzen. Dieser hängt zusätzlich davon ab, ob es im Fall einer positiven Diagnose überhaupt nachgewiesen wirksame Therapien gibt, um gegen die diagnostizierte Erkrankung vorzugehen, wie vielen Betroffenen damit geholfen werden könnte und welche Risiken damit für falsch-positive Fälle verbunden wären. Existiert beispielsweise noch keine evidenzbasierte Maßnahme, kann die diagnostische Testgüte noch so gut sein – eine frühe Diagnosestellung hat hier zunächst keinen Mehrwert, sondern führt nur dazu, dass Betroffene früher von ihrer Krankheit erfahren, ohne, dass sie etwas dagegen tun könnten. Die konkrete Nutzenbewertung eines diagnostischen Tests stellt indes ein weiteres komplexes Kapitel in der Berichterstattung über diagnostische Tests dar und wird deshalb in diesem Beitrag nicht mehr thematisiert.
Quellen:
Bremer, V. et. al. (2016) Abschlussbericht der Studie „Drogen und chronische Infektionskrankheiten in Deutschland“ (DRUCK-Studie). Robert Koch-Institut. DOI: 10.17886/rkipubl-2016-007.2
Deutsche AIDS-Hilfe e.V. (2017). HIV- und STI-Tests Informationen und Standards. Abgerufen von https://www.aidshilfe.de/shop/hiv-sti-tests-2017
Deutsches Netzwerk evidenzbasierte Medizin (2006): ebM-Splitter . Abgerufen von https://www.ebm-netzwerk.de/was-ist-ebm/splitter-zahnmedizin
EbM-Splitter 9 – Die Vierfeldertafel (in Diagnosestudien): Sensitivität und Spezifität
EbM-Splitter 10 Sensitivität und Spezifität: Auswirkung der Wahl des Trennpunktes
ebM-Splitter 11 – Nutzen einer diagnostischen Tests in der Praxis: prädiktive Werte
Deutsches Netzwerk evidenzbasierte Medizin (2016): Gute Praxis Gesundheitsinformation. Ein Positionspapier des Deutschen Netzwerks Evidenzbasierte Medizin e.V. (Version 2.0).
Gigerenzer, G. (2003). Wie kommuniziert man Risiken? Gen-ethischer Informationsdienst, 161, 1–6
Gigerenzer, G. et. al. (2000). Helping Doctors and Patients Make Sense of Health Statistics. Psychological Science in the Public Interest, 8 (2), 53-96. DOI: 10.1111/j.1539-6053.2008.00033.x
Gigerenzer, G., Hoffrage, U. & Ebert, A. (1998). AIDS counselling for low-risk clients. AIDS Care, 10 (2), 197-211.
Gigerenzer,G., Rebitschek, F.G. (2016). Informierte Patienten durch die Verbreitung von Faktenboxen. DOI: 10.17617/1.2O
Hinneburg, J., Wilhelm, C., Ellermann, C. (2018): Methodenpapier für die Entwicklung von Faktenboxen. Harding-Zentrum für Risikokompetenz, Max-Planck-Institut für Bildungsforschung. Abgerufen von https://www.harding-center.mpg.de/de/faktenboxen/methodenpapier-faktenboxen
Wegwarth, O. & Gigerenzer, G. (2011). Risikokommunikation: Unnötige Ängste vermeiden. Deutsches Ärzteblatt, 108 (17), A-943 / B-776 / C-776
Hinneburg, J., Wilhelm, C., Ellermann, C. (2018): Methodenpapier für die Entwicklung von Faktenboxen. Harding-Zentrum für Risikokompetenz, Max-Planck-Institut für Bildungsforschung. Abgerufen von https://www.harding-center.mpg.de/de/faktenboxen/methodenpapier-faktenboxen
https://evidenzgeschichten.podigee.io/14-falsche-sicherheiten
Tabelle und Grafiken: eigene Abbildung